Introduction to \LaTeX

Introduction to $\LaTeX$#

Supplemental Material
Last updated July 17, 2023

00. Content #

Mathematics

N/A

Programming Skills

Latex

Embedded Systems

N/A

0. Required Hardware #

N/A

1. A Very Brief Introduction to $\LaTeX$ #

$\LaTeX$ (pronounced “law-tek” or “lay-tek”) is a widely-used and well-established tool for creating beautifully typeset documents. It has been around for a long time and is commonly employed in various ways, such as:

writing submissions for academic journals
composing textbooks
preparing fiction books for publication
crafting assignments and exams for students
creating slide presentations (similar to PowerPoint)
writing personal letters to friends

Many mathematicians rely heavily on $\LaTeX$ when creating written documents. In this course, we will only utilize a small fraction of $\LaTeX$—specifically, the part that allows us to display formulas nicely. Markdown interpreters, including the one integrated with JupyterLab, have the capability to convert $\LaTeX$ expressions into beautifully rendered formulas. That’s how it is possible to present a formula like:

\[ e^x = \sum_{n=0}^\infty \frac{x^n}{n!} \]

By double-clicking on this cell, you can view the actual characters used to create the formula. Notably, the $$ markers are employed at the beginning and end to indicate the presence of a formula in Markdown.

Exercise 1 #

Copy and paste the formula from the cell above into the cell below. Change it so that instead of $x$, the variable is $y$.

Write Answers for Exercise 1 Below

One of the reasons why $\LaTeX$ is so popular is its ability to present the same formulas in different ways based on the context. If you want to include a formula within a line of text (without starting a new line), you can enclose the code with dollar signs ($) like this: $e^x = \sum_{n=0}^\infty \frac{x^n}{n!}$. Notice that the sum is displayed smaller to avoid disrupting the flow of the text, yet the code used remains the same.

Escape Sequences#

Many mathematical symbols that we commonly use are not readily available on a typical keyboard. For instance, if you want to use a lowercase sigma, you might not find it directly. However, in $\LaTeX$, you can represent a lowercase sigma by typing \sigma, which will be displayed as $\sigma$. Anything written after a backslash (symbol: \, typically found below the backspace key on most keyboards) is treated as a command rather than being printed directly. In this case, the command is to “insert a lowercase sigma here”. For a capital sigma, you can simply type \Sigma with a capital “S”, resulting in $\Sigma$.

Exercise 2 #

Write some LaTeX code in the cell below to produce a lowercase phi, psi, gamma, and delta, followed by uppercase versions of each.

Write Answers for Exercise 2 Below

Subscripts, Superscripts, and Grouping#

It is quite common in mathematics to express superscripts, such as the exponent $2$ in $x^2$ or the subscript $r$ in $\varepsilon_r$. This is achieved using the caret (^) and underscore (_) keys. However, it is important to note that LaTeX differs from Python syntax. In Python, we would write $x^2$ as x**2, so it’s crucial to avoid confusion when switching between the two.

Another aspect to be mindful of is that the superscript or subscript applies only to the immediate element following it. Consequently, if we attempt to raise $x$ to the 23rd power using a single caret (x^23), the result will be $x^23$, which is incorrect. To rectify this, we need to group the numbers $2$ and $3$ together using braces { and }, as in x^{23}, resulting in $x^{23}$.

Exercise 3 #

The formula below is all wrong! Put in braces to make it correct.

\[ \cos(x) = \sum_k=0^\infty \frac{(-1)^k x^2k}{(2k)!} \]

Write Answers for Exercise 3 Below

Fractions and Parentheses#

Fractions in LaTeX behave differently compared to regular symbols. When writing a fraction, such as \frac12, it affects the two symbols that follow it, resulting in $\frac12$. However, in most cases, fractions involve more than one character in the numerator and denominator, so it is recommended to use two pairs of braces, like \frac{1}{2}. This not only improves readability but also allows for more complex fractions, including fractions within fractions.

For example, consider the following formula:

\[ \frac{pq}{p+q} = \frac{1}{\frac{1}{p} + \frac{1}{q}} \]

When working in “text mode” (the smaller in-line text denoted by $), fractions appear smaller, while in “display mode,” they are larger by default. However, if you want to override this behavior, you can use the command \tfrac to consistently display smaller-style fractions or the command \dfrac to always use the display style.

In expressions involving fractions, the height of the expression can often exceed that of a single character, resulting in unappealing visuals.

\[\begin{align*} 1 = \sum_{n=1}^\infty (\frac{1}{2})^n \end{align*}\]

To address this, we can use the commands \left and \right to transform regular parentheses into scaling parentheses. For instance:

\[\begin{align*} 1 = \sum_{n=1}^\infty \left( \frac{1}{2} \right)^n \end{align*}\]

By using \left( and \right), the parentheses adjust their size to encapsulate the content within them, creating a more visually pleasing equation.

Getting Help#

Almost nobody knows every LaTeX command by heart. Fortunately, there are numerous ways to seek help on the internet. One popular tool for finding the escape sequence of a symbol is Detexify. Give it a try!

Exercise 4 #

Use Detexify to find the escape sequence for the symbol symbol , then type it using Latex below.

Write Answers for Exercise 4 Below

Another powerful way is to copy someone else’s working code. One great place to find it is on Wikipedia.

Exercise 5 #

You haven’t been informed yet about how to write a binomial coefficient in LaTeX. To figure it out, visit the Wikipedia page for the binomial theorem and locate the formula shown below:

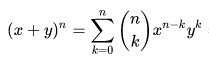
Access the “edit” section on the top-right of the Wikipedia page to copy the LaTeX code provided for reproducing the formula. Then, modify the index of summation from $k$ to $i$.