Week 5-6: Image Quantization

Week 5-6: Image Quantization#

Laboratory 3
Last updated July 24, 2023

00. Content #

Mathematics

Probability mass function
Cumulative distribution function

Programming Skills

Functions
Loops
Multi-dimensional arrays

Embedded Systems

Thonny and MicroPython

0. Required Hardware #

Raspberry Pi Pico
Breadboard
USB connector
Camera (Arducam HM01B0)
8 Wires

Write your name and email below:

Name:

Email:

1. Quantization #

In The Data Science Labs on Mulitvariable Calculus, we briefly introduce uniform quantization methods. Quantization of images refers to the process of reducing the information in an image from a wider range of values to a smaller range. Quantization is used for image compression to save storage space on devices, for creating image filters, and for processes like printing. As we saw observed in the previous lab on texture identification, grayscale images contain values between 0 and 255. However, what if we could only use 5 or 10 discrete values? In that case, we would require a mapping or function that transforms our original range of 0-255 to the 5 or 10 new discrete levels.

import numpy as np
import matplotlib.pyplot as plt    

num_levels=5
# creates a numpy array of (length num_levels + 1) evenly spaced floating points from 0 to 255
x = np.linspace(0,255,num_levels+1)
# # creates a numpy array of (length num_levels) evenly spaced floating points from 0 to 255
y = np.linspace(0,255,num_levels)
plt.step(x, np.append(y,y[-1]), where='post')
plt.xlabel('Grayscale Value')
plt.ylabel('Quantized Value')
plt.title(f'Uniform Quantization in 1D with {num_levels} Levels')
plt.show()

We can interpret uniform quantization from this graph. Given a image $I$ with dimensions $m\times n$, at each pixel location $(i,j)$, we have a grayscale value, which is an integer ranging from 0 to 255. Then, based on the graph, we modify the grayscale value at $(i,j)$ to a new value. For instance, with 5 quantization levels, if the original grayscale value is 40, we will change it to 0.

Exercise 1#

Write a function that takes in a grayscale image as a NumPy array and returns a uniformly quantized image with $k$ levels. Download low_contrast.jpg and show your results when $k=2,5,10,25$.

Write Answers for Exercise 1 Below

from PIL import Image                                   # needed for reading images

img = np.array(Image.open('low_contrast.jpg'))          # read in the image and store it as a numpy array
print(f'image size is {img.shape}')
fig, ax = plt.subplots(figsize=(12,6))                  # create figure and set figure size
ax.imshow(img, cmap='gray', vmin=0,vmax=255)            # display the image in grayscale between 0 and 255
ax.axis('off')                                          
plt.show()

# COMPLETE YOUR FUNCTION HERE
def uniform_quantization(img, k):
    return

# these are the test cases
'''
quantized_img = uniform_quantization(img, 2)            # uniform quantization with k = 2
fig, ax = plt.subplots(figsize=(12,6))                  # create figure and set figure size
ax.imshow(quantized_img, cmap='gray', vmin=0,vmax=255)            # display the image in grayscale between 0 and 255
ax.axis('off')                                          
plt.show()

quantized_img = uniform_quantization(img, 5)            # uniform quantization with k = 5
fig, ax = plt.subplots(figsize=(12,6))                  # create figure and set figure size
ax.imshow(quantized_img, cmap='gray', vmin=0,vmax=255)            # display the image in grayscale between 0 and 255
ax.axis('off')                                          
plt.show()

quantized_img = uniform_quantization(img, 10)           # uniform quantization with k = 10
fig, ax = plt.subplots(figsize=(12,6))                  # create figure and set figure size
ax.imshow(quantized_img, cmap='gray', vmin=0,vmax=255)            # display the image in grayscale between 0 and 255
ax.axis('off')                                          
plt.show()

quantized_img = uniform_quantization(img, 25)           # uniform quantization with k = 25
fig, ax = plt.subplots(figsize=(12,6))                  # create figure and set figure size
ax.imshow(quantized_img, cmap='gray', vmin=0,vmax=255)            # display the image in grayscale between 0 and 255
ax.axis('off')                                          
plt.show()
'''

Exercise 2#

Write a function that quantizes an image according to the power function shown below with $k$ levels and power $p$. This is an example of non-uniform quantization.

num_levels = 8
power = 4.0 
x = np.linspace(0,255,num_levels+1)
y = np.power( np.linspace(0, 255**(1/power), num=num_levels), power) 
  
plt.step(x, np.append(y,y[-1]), where='post')
plt.xlabel('Grayscale Value')
plt.ylabel('Quantized Value')
plt.title('Non-uniform Quantization in 1D')
plt.show()

Write Answer for Exercise 2 Below

# COMPLETE YOUR FUNCTION HERE
def power_quantization(img, k, p):
    return

2. Histogram Equalization #

Histogram equalization is an adaptive image processing method, which means that the transformation depends on the image itself. It is commonly used in medical imaging applications, as well as in scientific imaging fields such as astronomy and microbiology. In contrast to the non-adaptive uniform quantization method we discussed in the previous exercise, histogram equalization takes into account the specific characteristics of each image.

Let’s consider an image $I$ of size $m \times n$. We can determine the probability that a pixel value is at level $\ell$ by calculating the frequency of $\ell$ in the image. This probability, known as the probability mass function (pmf), can be expressed as:

\[ p_I(\ell) = \frac{\text{ \# of times $\ell$ appears in $I$}}{m\cdot n}\quad \text{ for } \ell = 0,1,2,\dots,255 \]

Furthermore, we can compute the cumulative distribution function (cdf) of $I$, denoted as $F_I(\ell)$, which represents the probaiblity that a pixel in I has a value less than or equal to $\ell$. The cdf is calculated as the cumulative sum of the pmf values:

\[ F_I(\ell) = \sum_{j=0}^\ell p_I(j) \quad \text{ for } \ell = 0,1,2,\dots,255\]

By analyzing the pmf and cdf of an image, we can gain insights into the distribution of pixel values and use this information to perform histogram equalization.

Exercise 3#

Plot the probability mass function and the cumulative distribution function of low_contrast.jpg.

Write Answers for Exercise 3 Below

Exercise 4 Part 1#

Plot the pmf and cdf of low_contrast.jpg after uniform quantization with $25$ levels.

Write Answers for Exercise 4 Part 1 Below

Exercise 4 Part 2#

Describe how the quantization process changed these two functions.

Write Answers for Exercise 4 Part 2 Below

Now, we will derive the method of histogram equalization.

We start with an image $I$ of size $m\times n$, and our objective is to define a mapping that transforms the original pixel intensities to new values. Let’s denote the transformed image as $I_{new}$.

The goal of histogram equalization is to distribute pixel intensities evenly across the entire range of values from 0 to 255. This means that $I_{new}$ will have an equal number of pixels at each intensity level, resulting in a flat probability mass function (pmf) for $I_{new}$.

Exercise 5#

If the pmf of $I_{new}$ is flat, how will the cdf of $I_{new}$ look? Why?

Write Answers for Exercise 5 Below

We can denote the cdf of $I_{new}$ by $ H(\ell) = \sum_{j=0}^\ell p_{I_{new}}(j) \quad \text{ for } \ell = 0,1,2,\dots,255 $

If $I_{new}$ has the same number of pixels at each intensity, then there are $\frac{m\cdot n }{255}$ pixels with a value of $\ell$ for $\ell = 0,1,2,\dots,255$.

Exercise 6#

Explain why $ H(\ell) = \frac{(\ell + 1) \cdot m\cdot n}{255} \quad \text{ for } \ell = 0,1,2,\dots,255 $

Write Answer for Exercise 6 Below

Now, in image $I$, the grayscale value 0 will change to some new value between $0$ and $255$. Since we haven’t defined the exact transformation map, let’s call that new level $n_0$. Similarly, we will change pixels in $I$ with the grayscale value 1 to some new value $n_1$. Pixels with value 2 in $I$ will change to the value $n_2$, and so on until we reach $n_{255}$.

In other words, in our transformed image $I_{new}$, we map the intensity levels $0,1,2,\dots,255$ in the original image $I$ to some new levels $n_0,n_1,n_2,\dots,n_{255}$.

We want the number of pixels with intensity between $0$ and $\ell$ in image $I$ to be the same as the number of pixels with intensity between $0$ and $n_\ell$ in image $I_{new}$.

By definition, $F_I(\ell)$ is the number pixels in $I$ with intensity between $0$ and $\ell$. Similarly, $H(n_\ell)$ is the number of pixels in $I_{new}$ with intensity between $0$ and $n_\ell$.

To determine the ideal levels $n_0,n_1,n_2,\dots,n_{255}$ that will even out the grayscale intensity in image $I$, we want to set $ F_I(\ell) = H(n_\ell)\quad \text{ for } \ell = 0,1,2,\dots,255. $

Exercise 7#

In the last line, evaluate the function $H$ at $n_\ell$ and solve for $n_\ell$. Format your answer using $\LaTeX$.

Write Answers for Exercise 7 Below

NOTE

This is a 2-week lab. Turn in the exercises above. Pick up from here during the next lab session.

Exercise 8#

Now that we know the values for $n_0,n_1,n_2,\dots,n_{255}$, we are ready to implement the histogram equalization process.

Implement histogram equalization on low_contrast.jpg. Plot the transformed image $I_{new}$ along with the pmf and cdf of $I_{new}$.

Hint: If the new levels $n_0,n_1,\dots,n_{255}$ are not integers (which is likely), then use np.floor function to round down.

Write Answers for Exercise 8 Below

3. Connecting the Camera #

This time, we will record our own videos using the Arducam HM01B0, which is a small camera that can be connected to the Pico.

Wiring Instructions#

Please ensure that your microcontroller is not connected to the computer while you are wiring components together. If you are unsure about your wiring, please consult the instructor. Use your jumper wires to establish the following connections:

HM01B0	Pico
VCC	3V3
SCL	GP5
SDA	GP4
VSYNC	GP16
HREF	GP15
PCLK	GP14
DO	GP6
GND	GND

Here is an image of the completed breadboard:

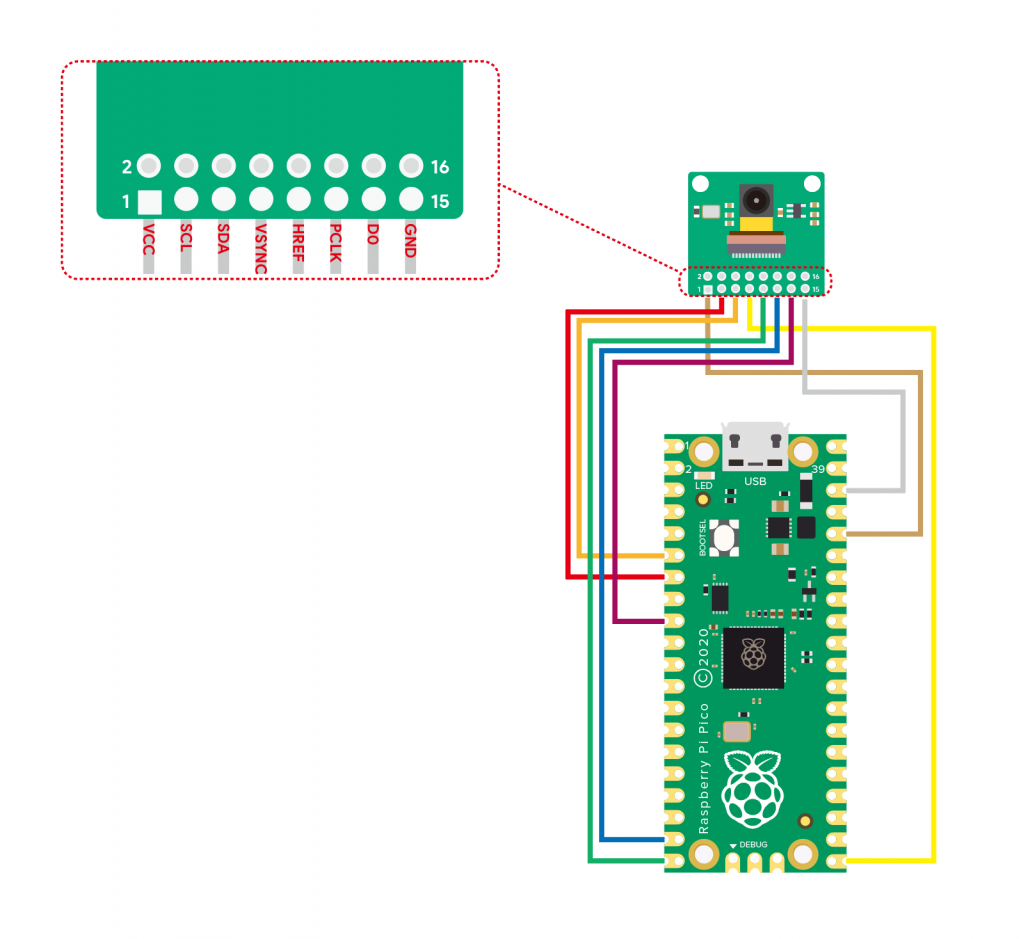
To find the names of the pins on the Raspberry Pi Pico, you can refer to its pinout diagram located here or in the Extra Materials section. The HM01B0, on the other hand, should have its pins labeled.

After confirming that the wiring is correct, press and hold the BOOTSEL button on the Pico while plugging it in. Download the arducam.uf2 file and copy it onto the Pico’s drive using your computer’s file manager (it should be listed as an external drive: “RPI-RP2”) and not with Thonny. Once the file transfer is complete, the Pico will automatically disconnect, and its LED will start blinking rapidly.

Once the Pico has been successfully connected, please execute the following cell to ensure that we have successfully detected the Pico.

import time
import serial
from serial.tools import list_ports

PICO_HWID = "2E8A"


def get_pico_port():
    pico_ports = list(list_ports.grep(PICO_HWID))
    if len(pico_ports) == 0:
        raise Exception(
            "No Raspberry Pi Pico was detected. Check to make sure it is plugged in, and that no other programs are accessing it"
        )
    return pico_ports[0].device


print("Here are all the serial devices detected:")
for port in list_ports.comports():
    print(port.device, port.hwid)

port = get_pico_port()
print(f"\nselected port {port} as most likely to have a raspberry pi pico")

Capturing a still image#

Now that the Pico and camera have been connected, execute the following cell to capture a still image.

buffer = bytearray(96 * 96)
img = np.zeros(shape=(96, 96), dtype="uint8")

with serial.Serial(port, timeout=1) as s:
    s.read_until(b"\x55\xAA")
    s.readinto(buffer)
    img.flat[::-1] = buffer

plt.imshow(img, cmap="gray")
plt.show()

Exercise 9#

Repeat the previous exercise using your own captured image from the Arducam HM01B0 connected to a Pico.

Write Answers for Exercise 9 Below

Exercise 10#

Can you think of any images that would not show significant improvement after applying histogram equalization?

Write Answer for Exercise 10 Below

Exercise 11#

What happens if we first quantize the image, either uniformly or non-uniformly, with $k$ levels and then apply the histogram equalization process? On the other hand, what happens if we apply histogram equalization first and then perform uniform or non-uniform quantization? How will increasing or decreasing the number of quantization levels $k$ change the new pmf and cdf?