Week 10: How Accurate is Your Height Measurement? (Derivative Rule for Error Propagation)

Week 10: How Accurate is Your Height Measurement? (Derivative Rule for Error Propagation)#

Laboratory 4d
Last updated Mar 21, 2023

00. Content #

Mathematics

Accuracy
Precision
Absolute error
Relative error
Combining errors
Error propagation
Partial derivatives

Programming Skills

Symbolic computation using SymPy

Embedded Systems

N/A

0. Required Hardware #

N/A

Copy the file `student_info.py` into the folder you are working in, then run this cell to put your name and email into this document.

from student_info import show_info
show_info()

1. The Plan #

In the previous lab, you collected data which will give us the heights of several buildings around campus. You identified several sources of error which may affect the accuracy of your results. This is typical: usually, error comes from more than one source. In this lab, you learn how to incorporate what you know about the errors in your measurements to get a numerical value for the error in your results.

2. A Review of Errors #

Exercise 1 (5 pts)#

In a sentence or two, write down the difference between random and systematic errors. Look at previous labs if you have forgotten.

Write Answers for Exercise 1 Below

Accuracy and precision#

The distinction between random and systematic errors is often phrased in terms of how accurate a measurement is and how precise a measurement is. Professional scientists and engineers use the words “accuracy” and “precision” to refer to two different, related concepts. Accuracy refers to how close the measurement is to the true value. Precision refers to how close repeated measurements are to each other. This is summarized in the following image – in this metaphor the arrows are our measurements, and the target is the true value.

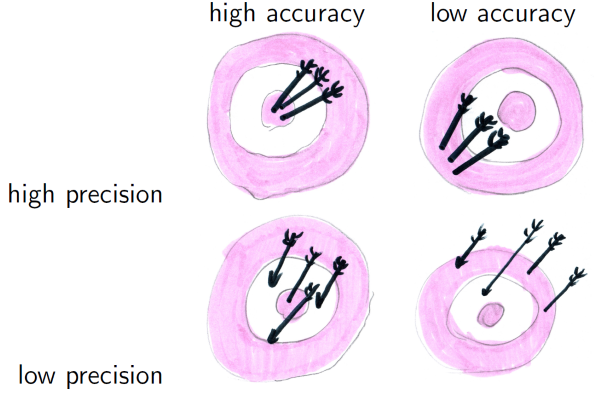
accuracy vs precision

In the terms described above, a measurement is accurate if $|\varepsilon|$ is small. A measurement is precise if $|\varepsilon|$ is close to its average value. It follows that the accuracy can only be as good as the precision, so we often do want to have good precision. However, as the picture shows, it is possible (and indeed, common) to have lots of precision but not much accuracy. In that case, the precision isn’t really doing you any good. The real goal is accuracy. Don’t lose sight of that!

Two ways of reporting errors#

So far we have been talking about the error $\varepsilon$ directly. This is also called the absolute error. This term has nothing to do with absolute value. Absolute error can be positive or negative. The units of absolute error are the same as the units of the measured quantity. A typical ruler has markings down to the 1/16 inch, so interpolating by eye you can make sure the error is less than 1/32 inches. This can be very good for measuring, say, how long your pencil is, since a typical pencil is around 7 inches long. The pencil on my desk is 7 1/8 inches long, $\pm$ 1/32 inch. I use the symbol $\pm$ to indicate that I don’t know whether my guess is too high or too low. All I can say for sure is $$ 7\frac{1}{8} -\frac{1}{32}< t < 7\frac{1}{8}+\frac{1}{32} $$

A ruler like this would not be as appropriate for measuring how wide the pencil is – it can only tell me it is 1/4 inch wide, $\pm$ 1/32 inch. To express this idea mathematically, we simply divide the error by the true value $x$ – or if we don’t know the true value, by our best guess. We write this as

\[\begin{align*} \eta = \frac{\varepsilon}{t} \approx \frac{\varepsilon}{x}, \end{align*}\]

using the greek letter eta ($\eta$) which also makes an “e” sound, though it looks sort of like a lowercase n. This quantity is called the relative error. Unlike the absolute error, the relative error is dimensionless – it would be the same if we expressed the answer in inches or centimeters or smoots. Relative error is usually expressed as a percentage. For example, the length of my pencil is 7 1/8 inches $\pm$ 0.44%. The width of my pencil is 1/4 inch $\pm$ 12.5%. This shows how a ruler is not appropriate for measuring the width of a pencil, but it’s fine for measuring the length – the relative error is significantly different.

We often want an equation relating $t$ and $x$ using the relative error instead of the absolute error. This is easily achieved by factoring:

\[\begin{align*} x &= t + \varepsilon\\ &= t\left(1+\frac{\varepsilon}{t}\right)\\ &=t(1+\eta) \end{align*}\]

Exercise 2 (10 pts)#

For each of the quantities expressed below, identify whether it is an absolute error or a relative error. Then, convert it to the other type of error. Make sure you are using appropriate units.

135 pounds $\pm$ 3 pounds
15 PSI $\pm$ 30%
22 hours $\pm$ 0.5%
3 weeks $\pm$ 4 days

Write Answers for Exercise 2 Below

Combined errors and significant figures#

Most calculations we do involve more than one number. Each number has its own error associated with it. As an example, suppose I measure the length of one pencil to be $x_1$, and another to be $x_2$ inches long. How long will they be together, put end to end? $y = x_1+x_2$, of course. How will the errors relate to each other? They will also add together. We can see this in a formula:

\[\begin{align*} (x_1+\varepsilon_1)+(x_2+\varepsilon_2) &= y+(\varepsilon_1+\varepsilon_2)\\ &=y+\varepsilon_{total} \end{align*}\]

The answer is of the form $y+\varepsilon_{total}$, where the total error is $\varepsilon_{total}=\varepsilon_1+\varepsilon_2$. So, when adding quantities with error, the absolute errors should add together.

Exercise 3 (5 pts)#

I measure the length of a rope by dividing it in two sections (so that I can use my measuring tape, which is shorter than the rope). The first part measures $311\pm 0.5$ inches, and the second measures $214 \pm 0.25$ inches. What is the length of the full rope, including the error?

Write Answers for Exercise 3 Below

Multiplication#

What about if the numbers are multiplied? For example, if you know the length and width of a rectangular sheet of paper, how do you find the error associated with calculating the area? Let’s try the formula again:

\[ (x_1+\varepsilon_1)(x_2+\varepsilon_2) = x_1x_2 +x_1\varepsilon_2 + x_2\varepsilon_1 + \varepsilon_1\varepsilon_2. \]

That is not such a tidy formula. There are a couple things we can do to make it easy on ourselves, though. For one thing, in any reasonable computation, the error is much smaller than the actual quantity being measured. It follows that the product of two errors should be much, much smaller than the product of the two quantities. Symbolically, we can write this as $\varepsilon_1\varepsilon_2<<x_1x_2$. So, we should be safe ignoring that term in the equation:

\[ (x_1+\varepsilon_1)(x_2+\varepsilon_2) \approx x_1x_2 +x_1\varepsilon_2 + x_2\varepsilon_1. \]

We can do better yet. Let’s do just a bit of factoring:

\[\begin{align*} x_1x_2 +x_1\varepsilon_2 + x_2\varepsilon_1 &= x_1x_2\left(1+\frac{\varepsilon_2}{x_2}+\frac{\varepsilon_1}{x_1}\right)\\ &=x_1x_2(1+\eta_2+\eta_1)\\ &=x_1x_2(1+\eta_{total}) \end{align*}\]

There is our rule! instead of the absolute errors adding together, the relative errors add when multiplying. This is another reason why relative error is so popular: it is easier to propagate a relative error through a product.

Exercise 4 (10 pts)#

I measured a page from my notepad. The width was $76\pm 0.25$ mm and the length was $118.5\pm 0.25$ mm. That means the width has a relative error of $\frac{0.25}{76}=0.33\%$.

Give the relative error of the length
Find the area of the notepad, assuming it is a rectangle. Give your answer with a relative error.
Besides the error in measuring the length and width, what other major form of error will affect the answer, if we take that as the area of the page?

Write Answers for Exercise 4 Below

3. The Derivative Rule for Error Propagation #

We have shared two rules for combining errors, when adding and when multiplying. There is just one more tool you need to be able to propagate errors through a great variety of computations. That is a general rule for how to propagate an error through a general function.

Errors in linear functions#

Let’s do the simplest function we can think of first. Suppose you know the absolute error in $x$ is $\varepsilon=0.1$ and we wish to know the error in computing $y=mx+b$. Let’s assume for now that $m$ is positive. The largest $x$ can possibly be is $x+0.1$, so the largest $y$ can be is $m (x+0.1)+b= mx+b+0.1m$. The smallest $x$ can be is $x-0.1$, so the smallest $y$ can be is $m (x-0.1) +b = mx+b-0.1m$. That is, we could write

\[\begin{align*} y= mx+b \pm 0.1m. \end{align*}\]

The absolute error was multiplied by the slope of the line; the intercept had nothing to do with it.

Exercise 5 (5 pts)#

The temperature outside is 42 degrees Fahrenheit, plus or minus one degree Fahrenheit. What is the temperature (with absolute error) in degrees Celsius?

Write Answers for Exercise 5 Below

4. Errors in General Functions #

If our computations are of any value at all, we have to assume that the input error is pretty small, compared with the other numbers in the computation. Therefore, if a function is differentiable, a linear approximation should be pretty good. That is,

\[ f(x+\varepsilon) \approx f(x) + f'(x)\varepsilon. \]

This lets us propagate errors through any function we can differentiate! Let’s do an example: if we measure $x=3\pm0.05$, what is $y=x^2+6x-3$ with the error? Our best estimate is $3^2+6\times 3-3=24$, and the error is $f'(3)0.05=12*0.05=0.6$. So, we should report the answer as $y=24\pm 0.6$.

Exercise 6 (5 pts)#

For each function and measurement below, report the value of the result with its error.

$x=\pi/6\pm 0.2$, $y=\sin(x)$
$x=2\pm 0.05$, $y=e^x$
$x=3\pm 0.01$, $y=x^2$
$x=3\pm 1\%$, $y=x^2$

Write Answers for Exercise 6 Below

5. A Caution About Small Derivatives #

Here is an example which shows the limitations of this strategy. What if $x=0\pm 0.1$, and $y=\cos(x)$? This approximation would tell you the error should be $0.1f'(0)=-0.1\sin(0)=0$. Is it accurate to say the error is zero in this case? That was a rhetorical question. The answer is no.

Exercise 7 (10 pts)#

Explain why it would be wrong to say the error is zero in this case. What is the smallest number $y$ could be? What is the biggest number $y$ could be? Answer in at least 3 sentences.

Write Answers for Exercise 7 Below

How to make the method work, even if the derivative is zero#

This method of error propagation is based on the approximation $ f(x+\varepsilon) \approx f(x) +f'(x)\varepsilon. $ If you know Taylor series, you can probably come up with an even better approximation involving $f''(x)$. We won’t explore that any further today, but it is good to be aware of it.

6. Analyzing the Height Measurements #

Remember the formula we introduced in the previous lab for the height of a building, $ h = \frac{r}{\cot \theta -\cot \phi}+k. $ This depends upon four different values, $r$, $k$, $\theta$, and $\phi$. Besides modeling error, every error in our measurement is due to error in one of these values.

Exercise 8 (20 pts)#

Identify three sources of error which affected your measurement of $r$, and give an estimate of the magnitude of each error. Identify the biggest source of error in your measurement of $k$.

Give the errors in $r$ and $k$ as both relative and absolute errors.

Write Answers for Exercise 8 Below

Errors in angle measurements#

There are a few things which can affect the precision of $\theta$ and $\phi$. This is compounded by the fact that, depending on how you chose to design your inclinometer, you might be using different components of acceleration to do your computation. We will work through an example together, but keep in mind that your formulas might be different.

One way to compute the angle would be $ \theta = \arctan \frac{\sqrt{a_x^2 + a_z^2}}{a_y}. $ Let’s say you have only three digits for each component – so, the error in each component of acceleration is $\pm 0.001$ gravities of acceleration. What would be the error in $\theta$? Let’s take some derivatives. First, let’s find the error due to $a_x$. We will apply the derivative rule. When taking the derivative, we will treat the other numbers as constants. Depending on your background in calculus, you may recognize this as a “partial derivative”. Here is what we find:

\[\begin{align*} \text{Error due to }a_x &= \frac{\partial \theta}{\partial a_x} \varepsilon_x \\ &= \frac{a_x a_y \varepsilon_x}{ \left(a_y^2 + a_x^2 + a_z^2\right) \sqrt{a_x^2 + a_z^2}}. \end{align*}\]

Some things make this nicer, like we know that there is one gravity of acceleration total, so $\left(a_y^2 + a_x^2 + a_z^2\right)=1$. That lets us simplify to

$ \text{Error due to }a_x = \frac{a_x a_y \varepsilon_x}{\sqrt{a_x^2 + a_z^2}}. $

Exercise 9 (10 pts)#

Write some code to compute this error for the specific values

\[\begin{align*} a_x &= 0.608\\ a_y &= 0.839\\ a_z &= 0.033\\ \varepsilon_x &= 0.001, \end{align*}\]

which I collected using my own inclinometer. As always, the number that calculus gives is in radians. Convert the answer to degrees; your answer should be about 0.05 degrees.

Write Answers for Exercise 9 Below

The partial derivative rule#

Of course, the other components of acceleration will also affect the angle measurement. We can just add these to the error, to get an estimate of the total error:

$ \varepsilon_\theta = \frac{\partial \theta}{\partial a_x} \varepsilon_x + \frac{\partial \theta}{\partial a_y} \varepsilon_y + \frac{\partial \theta}{\partial a_z} \varepsilon_z. $

We don’t know if the errors $\varepsilon_x$, $\varepsilon_y$, and $\varepsilon_z$ are positive or negative. To be safe, we should take the absolute value of each term:

$ \varepsilon_\theta = \left|\frac{\partial \theta}{\partial a_x}\right| \varepsilon_x + \left|\frac{\partial \theta}{\partial a_y}\right| \varepsilon_y + \left|\frac{\partial \theta}{\partial a_z}\right| \varepsilon_z. $ This is the partial derivative rule for error propagation.

Using the same values as exercise 9, this gives $\varepsilon_\theta = 0.09$ degrees.

Exercise 10 (25 pts)#

What do you think of this number? When you took your measurements, do you think you managed to orient your inclinometer to within a tenth of a degree?

In three to five sentences, explain what happened here using the language of accuracy and precision. How precise is this method you used, and how accurate?

Make a better estimate for $\varepsilon_\theta$, based on how accurately you think you were holding the inclinometer during measurement. give your estimate in degrees and in radians.

Write Answers for Exercise 10 Below

7. A Final Error Estimate #

Now we have values for $\varepsilon_r$, $\varepsilon_k$, $\varepsilon_\theta$, and $\varepsilon_\phi$ (we can use the same estimate for $\varepsilon_\theta$ and $\varepsilon_\phi$). We can apply the partial derivative rule to find the total error in our measurement of height:

$ \varepsilon_h = \left|\frac{\partial h}{\partial r}\right| \varepsilon_r + \left|\frac{\partial h}{\partial k}\right| \varepsilon_k + \left|\frac{\partial h}{\partial \theta}\right| \varepsilon_\theta + \left|\frac{\partial h}{\partial \phi}\right| \varepsilon_\phi. $

Let’s not take all those derivarives by hand. In the next lab, we will show a tool called “Sympy”, which is used for doing symbolic computations in Python. Just as a demonstration, here is how we can use it to find these derivatives without much work.

import sympy
from sympy.abc import r, k, theta, phi

h = r/(sympy.cot(theta)-sympy.cot(phi)) + k
h

h.diff(r)

h.diff(k)

h.diff(theta).simplify()

h.diff(phi).simplify()

Particularly with some of these trig functions, this can be a good way to prevent arithmetic errors. Here is what we just computed:

\[\begin{align*} \frac{\partial h}{\partial r} &= \frac{1}{\cot\theta-\cot\phi}\\ \frac{\partial h}{\partial k} &= 1\\ \frac{\partial h}{\partial \theta} &= \frac{r}{\sin^2\theta (\cot\theta-\cot\phi)^2}\\ \frac{\partial h}{\partial \phi} &= -\frac{r}{\sin^2\phi (\cot\theta-\cot\phi)^2}. \end{align*}\]

Combining these with the partial derivative rule (and assuming $\varepsilon_\theta = \varepsilon_\phi$), we get: $ \varepsilon_h = \frac{1}{\cot\theta-\cot\phi} \varepsilon_r + \varepsilon_k + \frac{r\left(\csc^2\theta+\csc^2\phi\right)}{(\cot\theta-\cot\phi)^2} \varepsilon_\theta. $

Exercise 11 (45 pts)#

Copy the code you wrote in lab 4c to load up the actual values you measured. Use the above formula to find, for each measurement, the error due to $r$, $k$ and $\theta$. Report all the heights you got together with their combined error. Write a two-paragraph summary of your findings, mentioning which source of error had the biggest effect on your measurement. Which of your measurements was the most precise? The least precise?